| Home» Third Temple |
The Temple
And it shall come to pass in the last days that the mountain of the house of Hashem shall be established at the top of the mountains, and shall be exalted above the hills; and all of the nations shall flow unto it. And many people shall go and say, Come, and let us go up to the mountain of the Lord, to the house of the God of Jacob; and He will teach us of His ways, and we shall walk in His paths: for out of Zion shall go forth Torah, and the word of God from Jerusalem. (Isaiah 2:2-3).
Next we show the two most statistically significant tables of these key words taken three at a time.

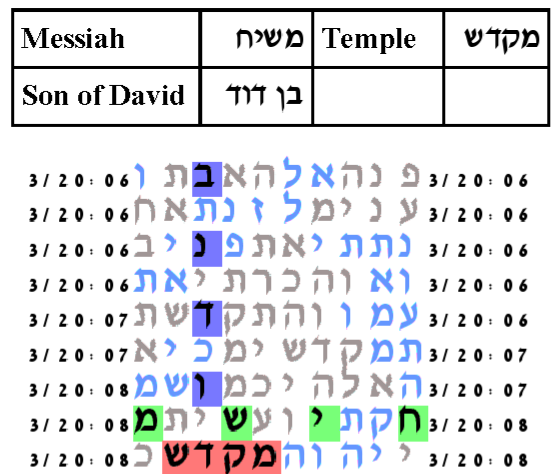
Art Levitt found a configuration of ELSs for the three key words Messiah, Temple, and Moriah. This configuration is also a smallest area configuration. In addition, it is a configuration that shows the ELSs for Temple and Messiah to be one column apart and parallel with the same skip.

There are two other tables having ELSs of the three key words Messiah, Temple, and Moriah. One of them also has a parallel geometry.

What is remarkable is that there is a compact table containing ELSs of each of the five key words we have been working with. Indeed, it was this table that motivated our study of the key word pairs and triples. For it is not generally the case that key words whose ELSs appear as a single table have significantly compact ELS meetings when taken as pairs or triples. Our study showed that in fact in this case the pairwise meetings, taken as a whole, are unexpectedly compact. If these five key words can be considered as a priori, the probability that a text from the ELS random placement text population would have as small an area table containing ELSs of these five key words is less than 1/100,000.

- <<< Previous
- 1
- 2
- 3


 Documentaries and Tutorials
Documentaries and Tutorials
