| Home»China's Massive Earthquake» The Wenchuan Earthquake |
The Wenchuan Earthquake
Up to this point, for the choice of key words we have tried, we have only found weak statistical evidence for an encoding of the Wenchuan earthquake. Rabbi Glazerson suggested trying the key word In China in place of China. We repeated our experiment using the date and year separately using the key word In China. As in the previous compound experiment, the date had six forms and was not grouped with the year and the year had two forms and was not grouped with the date. Two out of the six date subexperiment produced statistically signficant results. One subexperiment that was statistically significant used the form 7th of Iyar with Iyar spelled with a single Yod. The other subexperiment that was statistically signficant used the form 7th of Iyar for the date with Iyar spelled with a double Yod.
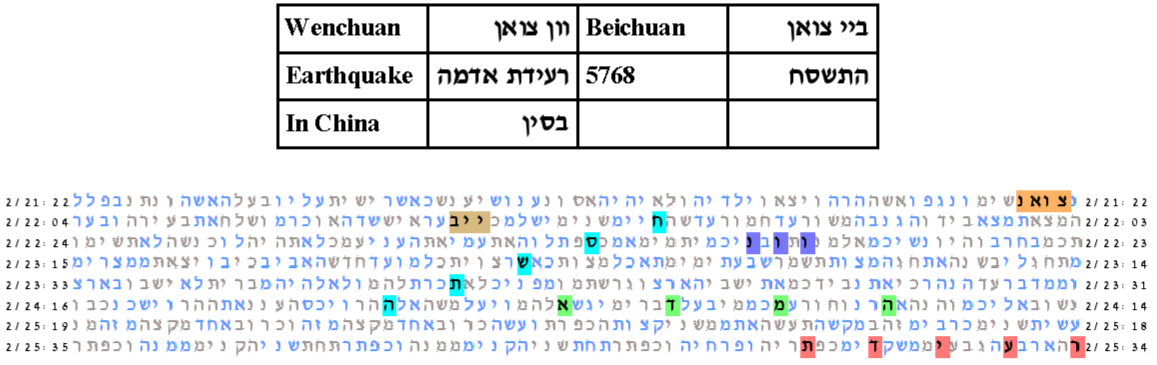
The best table is in an area not seen before from the previous experiments. With expected number of ELSs set to 75, the probability that a text from the ELS random placement text population would produce a table as compact as that produced by the Torah text is 8.5/1,000.
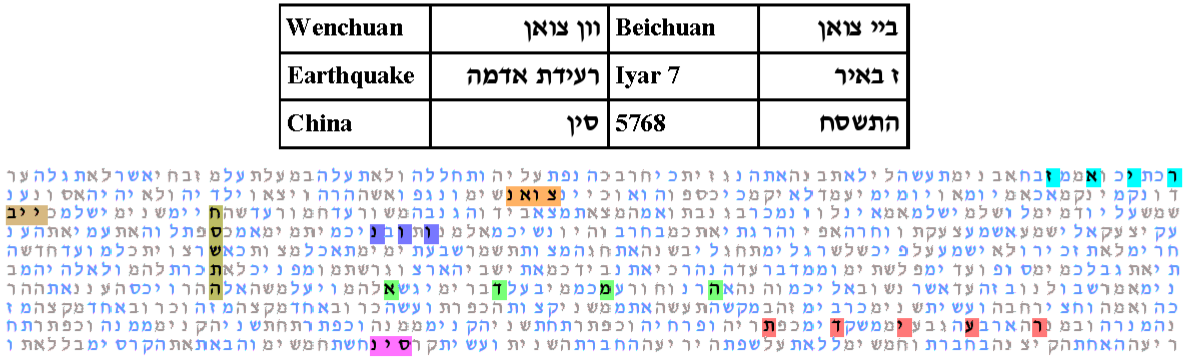
The second best table is located the same place as the best table of the previous experiment using the date. With expected number of ELSs set to 75, the probability that a text from the ELS random placement text population would produce a table as compact as that produced by the Torah text is 12.5/1,000.
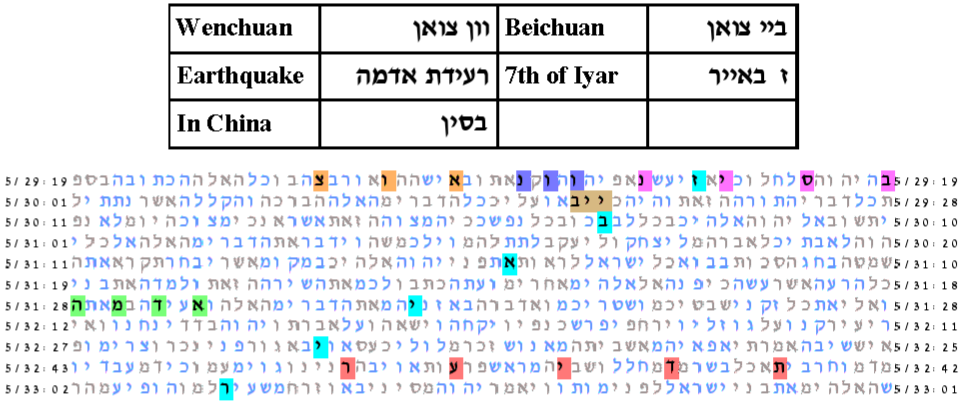
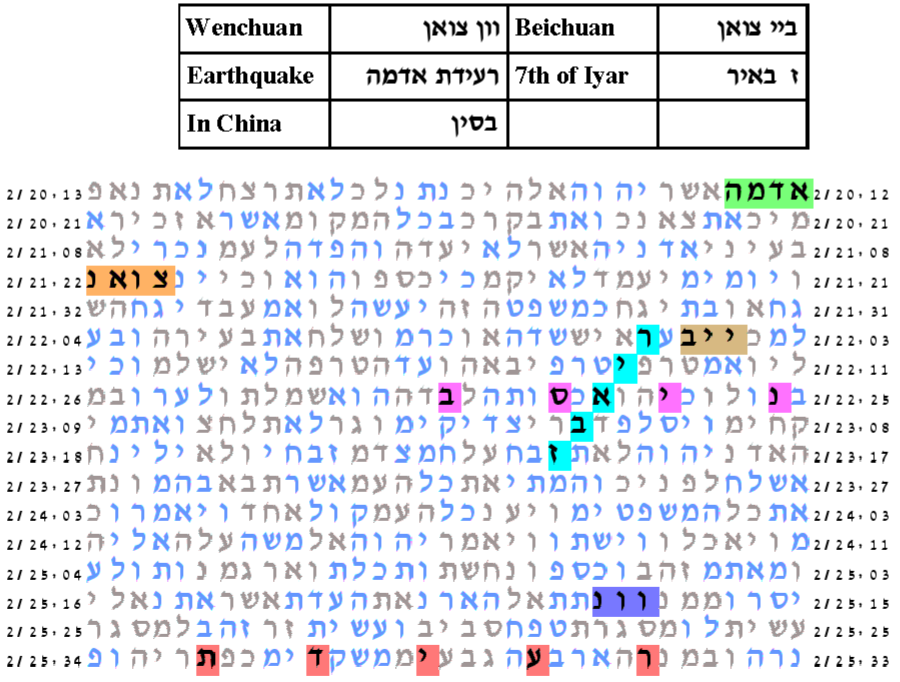
The best result for the year experiment used the form 5768. With expected number of ELSs set to 75, the probability that a text from the ELS random placement text population would produce a table as compact as the Torah text is 107.5/1,000. The table is a horizontally long and must be shown split in its left part and its right part.

We combine the results from the two experiments in our standard way to form a single score for each trial. We test the Null hypothesis against the alternative that one subexperiment from each experiment would produce a more compact result than expected by chance. With expected number of ELSs set to 75, the probability that a text from the ELS random placement text population would produce as good a score as the Torah text is 39.5/1,000.
Now it becomes clear what the strategy ought to have been from the beginning. The date experiment pairs best with the key word In China and the year experiment pairs best with the key word China. Therefore, the key word set should have required the key words Earth Quake, Wen Chuang, Bei Chuang, one of China or In China. For the date experiment it should have required one of the six forms of the date Iyar 7. And for the year experiment it should have required one of the two forms of the year 5768. Thus the compound experiment should have had 12 subexperiments associated with the date part and 4 subexperiments associated with the year part. The test should be of the Null hypothesis of no Torah code effect against the alternative hypothesis that one of the 12 subexperiments for the date and one of the 4 subexperiments for the year have ELSs that are more compact than would be expected by chance. If we had done such a compound experiment, where a score is associated with each trial, with expected number of ELSs set to 75, the probability that a text from the ELS random placement text population would produce a better score than that produced by the Torah text is 13.5/1,000, a statistically significant result.
We try another experiment in which we require both the date and the year to be in the table. We have six forms for the date and 2 forms for the year so the experiment has 12 subexperiments. With the expected number of ELSs set to 75, the probability that a text from the ELS random placement text population would produce a table as compact as that produced by the Torah text is 44.5/1,000.


 Documentaries and Tutorials
Documentaries and Tutorials