| Home» Hashem Appeared |

|
Hashem Appeared
We now explore deeper.
The subject of וירא may be with respect to יהוה directly
(Genesis 12:7, 17:1, 18:1, 26:2, 26:4; Deuteronomy 31:15) or indirectly
by reference to כבוד,
glory, (Leviticus 9:6, 9:23; Numbers 16:19, 17:7,20:6)
or מלאך,
angel (Exodus 3:2). When it is directly, the Torah's word immediately after וירא is יהוה (Genesis 12:7, 17:1; Deuteronomey 31:15) or אליכם (Leviticus 9:6) אליו (Genesis 18:1, 26:2, 26:4).
If the word immediately following is אליכם or אליו, then the next word is יהוה.
Therefore, we set up an experiment that uses for the first key word one of the
phrases ויראיהוה, ויראכבוד, ויראמלאך, ויראאליכם,
or ויראאליו.
For the second key word we use אור, light, םאור, from light, or באור, in light.
There are thus five groups of three key word pairs. We test the hypothesis of no Torah code effect
against the alternative hypothesis that for each of these five groups one of its three key word
pairs is encoded. The p-value of the test was 4.5/1000.
We next show each of the configurations whose individual p-values were less than .5.
There were ten such configurations.
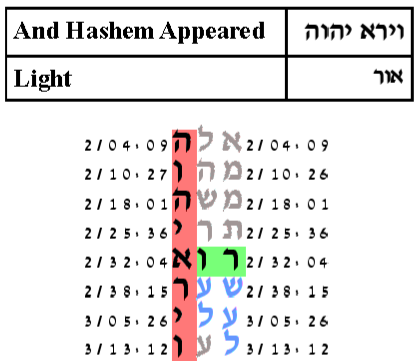
The expected number of ELSs was set to 50.
This is a smallest possible configuration.
The probability that a text from the ELS random placement text population would produce
such a smallest possible configuration is 171/1,000.
Finding by Professor Haralick

The expected number of ELSs was set to 50.
The probability that a text from the ELS random placement text population would produce
a configuration as compact as this is 15.5/1,000.
Finding by Professor Haralick
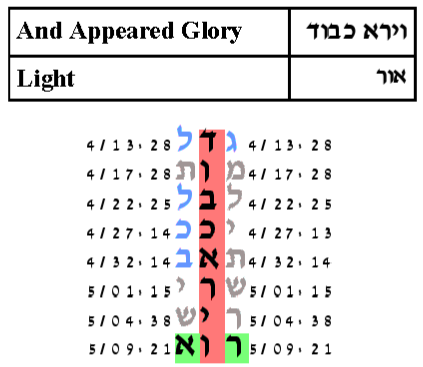
The cylinder size is 8,029 columns.
The expected number of ELSs was set to 50.
The probability that a text from the ELS random placement text population would produce
a configuration as compact as this is .5/1,000.
Finding by Professor Haralick

The cylinder size is 8,027 columns.
The expected number of ELSs was set to 50.
The probability that a text from the ELS random placement text population would produce
a configuration as compact as this is 459.5/1,000.
Finding by Professor Haralick
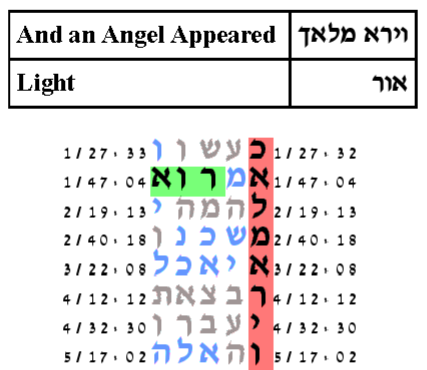
The cylinder size is 34,400 columns.
The expected number of ELSs was set to 50.
The probability that a text from the ELS random placement text population would produce
a configuration as compact as this is 468/1,000.
Finding by Professor Haralick

The cylinder size is 8,175 columns.
The expected number of ELSs was set to 50.
The probability that a text from the ELS random placement text population would produce
a configuration as compact as this is 320.5/1,000.
Finding by Professor Haralick
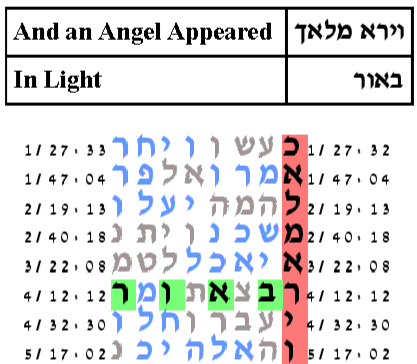
The cylinder size is 34,300 columns.
The expected number of ELSs was set to 50.
The probability that a text from the ELS random placement text population would produce
a configuration as compact as this is 351/1,000.
Finding by Professor Haralick

The cylinder size is 2,090 columns.
The expected number of ELSs was set to 50.
The probability that a text from the ELS random placement text population would produce
a configuration as compact as this is 243.5/1,000.
Finding by Professor Haralick

The cylinder size is 10,634 columns.
The expected number of ELSs was set to 50.
The probability that a text from the ELS random placement text population would produce
a configuration as compact as this is 287.5/1,000
Finding by Professor Haralick

The cylinder size is 10,634 columns.
The expected number of ELSs was set to 50.
The probability that a text from the ELS random placement text population would produce
a configuration as compact as this is 48.5/1,000.
Finding by Professor Haralick











 Documentaries and Tutorials
Documentaries and Tutorials